JDK-PriorityQueue原理

研究了二叉堆实现原理，现在来看看JDK里面基于二叉堆的优先队列怎么实现的！

关键点：基于priority heap，无界队列，实现Queue,Collection,Iterator接口、不允许null键/值、非线程安全、enqueue和dequeue都是O(long(n))，remove和contains是O(n)，peek是O(1)；

从PriorityQueue的概念，结构，参数，源码解析（offer,poll,remove,add,grow），性能，线程安全性，使用场景，常见问题8个方面进行分析。

概念

• 优先队列跟普通的队列不一样，普通队列遵循FIFO规则出队入队，而优先队列每次都是优先级最高出队。
• 优先队列内部维护着一个堆，每次取数据的时候都从堆顶取，这是优先队列的基本工作原理。

• jdk的优先队列使用PriorityQueue这个类，使用者可以自己定义优先级规则。

• An unbounded priority queue based on a priority heap.

• The elements of the priority queue are ordered according to their natural ordering, or by a Comparator provided at queue >construction time, depending on which constructor is used.
• A priority queue does not permit null elements.
• A priority queue relying on natural ordering also does not permit insertion of non-comparable objects (doing so may result in >ClassCastException).
• The head of this queue is the least element with respect to the specified ordering. If multiple elements are tied for >least value, the head is one of those elements — ties are broken arbitrarily.
• The queue retrieval operations poll, remove, peek, and element access the element at the head of the queue.
• A priority queue is unbounded, but has an internal capacity governing the size of an array used to store the elements on >the queue. It is always at least as large as the queue size. As elements are added to a priority queue, its capacity grows >automatically. The details of the growth policy are not specified.
• This class and its iterator implement all of the optional methods of the Collection and Iterator interfaces.
• The Iterator provided in method iterator() is not guaranteed to traverse the elements of the priority queue in any particular >order. If you need ordered traversal, consider using Arrays.sort(pq.toArray()).
• Note that this implementation is not synchronized. Multiple threads should not access a PriorityQueue instance concurrently if >any of the threads modifies the queue. Instead, use the thread-safe PriorityBlockingQueue class.
• Implementation note: this implementation provides
  • O(log(n)) time for the enqueuing and dequeuing methods (offer, poll, remove() and add);
  • linear time for the remove(Object) and contains(Object) methods;
  • constant time for the retrieval methods (peek, element, and size).
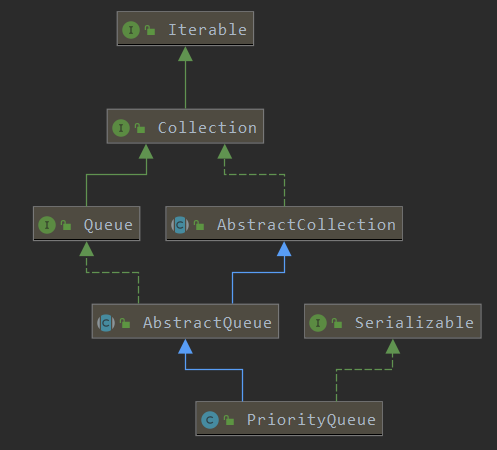
    This class is a member of the Java Collections Framework.

PriorityQueue的类关系

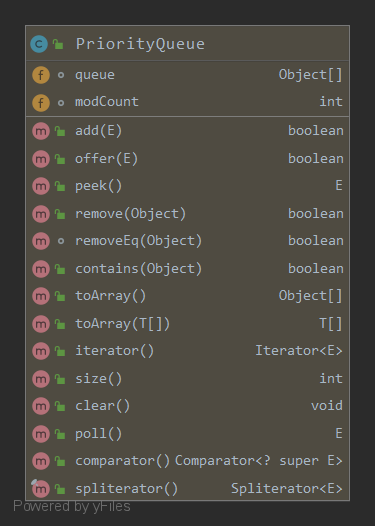
PriorityQueue的类成员

结构

一维数组

• Priority queue represented as a balanced binary heap:
• the two children of queue[n] are queue[2n+1] and queue[2(n+1)].
• The priority queue is ordered by comparator, or by the elements’ natural ordering,
• if comparator is null: For each node n in the heap and each descendant d of n, n <= d.
• The element with the lowest value is in queue[0], assuming the queue is nonempty.

  // non-private to simplify nested class access
  transient Object[] queue;

参数

• initialCapacity：初始化容量，默认为11；
• comparator:用于队列中元素排序；
• size:记录队列中元素个数；
• modCount:记录队列修改次数；
• 构造函数：新建1个空的队列；

  public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) {
      this.queue = new Object[initialCapacity];
      this.comparator = comparator;
  }

• 如果是由SortedSet,PriorityQueue这种有序的结构构建优先队列，直接Arrays.copyOf把数据复制到queue数组中；
• 如果是由无序数组构建优先队列，需要把数据复制到queue数组中后，执行构建堆(heapify)操作；

源码解析

heapify-构建堆

/**
 * Establishes the heap invariant (described above) in the entire tree,
 * assuming nothing about the order of the elements prior to the call.
 */
@SuppressWarnings("unchecked")
private void heapify() {
    //从最后一个非叶子节点（父亲节点）开始遍历所有父节点，直到堆顶
    for (int i = (size >>> 1) - 1; i >= 0; i--){
        //下沉（将3 or 2者中较大元素下沉）
        siftDown(i, (E) queue[i]);
    }
}

siftDown-下沉

/**
 * Inserts item x at position k, maintaining heap invariant by demoting x down the tree repeatedly
 * until it is less than or equal to its children or is a leaf.
 *
 * @param k the position to fill
 * @param x the item to insert
 */
private void siftDown(int k, E x) {
    if (comparator != null) {
        //按自定义顺序swap下沉
        siftDownUsingComparator(k, x);
    } else {
        //按字典顺序swap下沉
        siftDownComparable(k, x);
    }
}

按字典顺序swap下沉

@SuppressWarnings("unchecked")
private void siftDownComparable(int parent, E x) {
    Comparable<? super E> parentVal = (Comparable<? super E>) x;
    int half = size >>> 1;
    //二叉树结构，下标大于size/2都是叶子节点，其他的节点都有子节点。
    //循环直到k没有子节点：loop while a non-leaf
    while (parent < half) {
        //假设left节点为child中的最小值节点
        int left = (parent << 1) + 1;
        int right = left + 1;
        Object minVal = queue[left];
        //存在right，且right<left，则最小为right
        if (right < size && ((Comparable<? super E>) minVal).compareTo((E) queue[right]) > 0) {
            left = right;
            minVal = queue[right];
        }
        //如果parent节点<min(left,right),则不需要swap
        if (parentVal.compareTo((E) minVal) <= 0) {
            break;
        }
        //否则swap parent节点和min(left,right)的节点
        queue[parent] = minVal;
        //当前父节点取最小值的index继续loop
        parent = left;
    }
    //1.当前节点没有子节点，则k是叶子节点的下标，没有比它更小的了，直接赋值即可
    //2.当前节点下沉n轮后，将节点的值放到最终不需要再交换的位置（没有比它更小的或者到达叶子节点）
    queue[parent] = parentVal;
}

按自定义顺序swap下沉，与siftDownComparable类似

@SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        int child = (k << 1) + 1;
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = x;
}

offer

/**
 * The number of times this priority queue has been structurally modified 
 */
transient int modCount = 0;

/** 
 * 节点插入到队列 
 */
public boolean offer(E e) {
    if (e == null) {
        throw new NullPointerException();
    }
    //修改次数+1
    modCount++;
    int i = size;
    if (i >= queue.length) {
        //队列已满时，按50%动态扩容
        grow(i + 1);
    }
    size = i + 1;
    if (i == 0) {
        //队列为空时
        queue[0] = e;
    } else {
        //上浮调整堆顺序
        siftUp(i, e);
    }
    return true;
}

队列已满时，动态扩容：小于64时2倍扩容，大于64时0.5倍扩容；

/**
 * Increases the capacity of the array.
 *
 * @param minCapacity the desired minimum capacity
 */
private void grow(int minCapacity) {
    int oldCapacity = queue.length;
    // Double size if size<64; else grow by 50%
    int newCapacity = oldCapacity + (
        (oldCapacity < 64) ? (oldCapacity + 2) :(oldCapacity >> 1)
        );
    // overflow-conscious code 防越界
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
    //将queue中数据复制到扩容后的queue
    queue = Arrays.copyOf(queue, newCapacity);
}

private static int hugeCapacity(int minCapacity) {
    // overflow
    if (minCapacity < 0) {
        throw new OutOfMemoryError();
    }
    return (minCapacity > MAX_ARRAY_SIZE) ?
            Integer.MAX_VALUE :
            MAX_ARRAY_SIZE;
}

节点上浮调整

/**
 * Inserts item x at position k, 
 * maintaining heap invariant by promoting x up the tree until it is greater than or equal to its parent, or is the root. 
 * 为保持堆的性质，将插入元素x一路上浮，直到满足x节点值>=父节点值，或者到达根节点；
 * @param k the position to fill 插入位置
 * @param x the item to insert 插入元素
 */
private void siftUp(int k, E x) {
    if (comparator != null) {
        siftUpUsingComparator(k, x);
    } else {
        siftUpComparable(k, x);
    }
}

按字典顺序swap上浮

@SuppressWarnings("unchecked")
private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    //从当前节点循环上浮到堆顶节点
    while (k > 0) {
        //k节点的父节点索引
        int parent = (k - 1) >>> 1;
        //k节点的父节点值
        Object e = queue[parent];
        //比较k节点与父节点的值大小，父节点值较小时，终止遍历
        if (key.compareTo((E) e) >= 0) {
            break;
        }
        //父节点值较大时，交换k节点与父节点值
        queue[k] = e;
        //当前节点移到父节点，继续向上遍历
        k = parent;
    }
    //将当前节点值赋给交换后的父节点
    queue[k] = key;
}

按自定义顺序swap上浮，与siftUpComparable类似

@SuppressWarnings("unchecked")
private void siftUpUsingComparator(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

add

public boolean add(E e) {
    return offer(e);
}

remove

/**
 * Removes the ith element from queue.
 * <p>
 * Normally this method leaves the elements at up to i-1,
 * inclusive, untouched.  Under these circumstances, it returns null.
 * Occasionally, in order to maintain the heap invariant,
 * it must swap a later element of the list with one earlier thani.
 * Under these circumstances,
 * this method returns the element that was previously at the end of the list and is now at some position before i.
 * This fact is used by iterator.remove so as to avoid missing traversing elements.
 */
@SuppressWarnings("unchecked")
private E removeAt(int i) {
    assert i >= 0 && i < size;
    // 修改次数+1
    modCount++;
    // 堆尾元素Index
    int s = --size;
    if (s == i) {
        //如果删除的是堆尾元素，不需要进行siftUp
        queue[i] = null;
    } else {
        //拿出堆尾元素
        E moved = (E) queue[s];
        queue[s] = null;
        //将堆尾元素放到要删除的元素的位置，并执行siftDown
        siftDown(i, moved);
        //siftDown后，若元素没有改变，可能是因为要删除的结点和堆尾结点是跨子树，或者要删除的结点是叶子结点
        if (queue[i] == moved) {
            //如果删除的元素和堆尾元素不在一个子树，需要siftUp操作
            siftUp(i, moved);
            if (queue[i] != moved) {
                return moved;
            }
        }
    }
    return null;
}

注意

• 普通元素删除，将堆尾元素和要删除的位置替换，然后siftDown就可以；
• 但当删除的元素和堆尾元素之间如果是跨子树的话，需要从删除位置执行siftUp操作；
  示例

        0
    4       1
  5   6   2   3

  删除5，siftdown后

        0
    4       1
  3   6   2

  此时还需要siftup一次，才能满足二叉堆的结构

        0
    3       1
  4   6   2

poll

public E poll() {
    if (size == 0)
        return null;
    //queue修改次数+1
    modCount++;
    //堆顶元素
    E result = (E) queue[0];

    //堆尾索引
    int s = --size;
    //堆尾元素
    E x = (E) queue[s];
    //置空堆尾元素
    queue[s] = null;
    if (s != 0) {
        //堆尾元素拿出作为堆顶值后，从堆顶执行下沉
        siftDown(0, x);
    }
    //返回堆顶元素
    return result;
}

peek

public E peek() {
    //返回堆顶元素
    return (size == 0) ? null : (E) queue[0];
}

性能

参考二叉堆性能

• O(log(n)) time for the enqueuing and dequeuing methods (offer, poll, remove() and add);
• linear time for the remove(Object) and contains(Object) methods;
• constant time for the retrieval methods (peek, element, and size).

  线程安全性

  并发修改队列时非线程安全，线程安全版本使用PriorityBlockingQueue

  使用场景

  PriorityQueue处理优先级场景

  如医院急诊科接诊要按病痛的优先级处理；构建好优先队列后逐个poll即可；

PriorityQueue求TopK大/小的元素

使用小顶堆来实现TopK问题求解：维护一个大小为K的最大堆，那么在堆中的数都是TopK。

• 处理过程：在添加一个元素之后，如果小顶堆的大小大于 K，那么需要将小顶堆的堆顶元素去除
• 时间复杂度：O(Nlog(K))
• 空间复杂度： O(K)
• 特别适合处理海量数据

在海量数据场景下，单机通常不能存放下所有数据。

• 拆分：可以按照哈希取模方式拆分到多台机器上；在每个机器上维护最大堆；
• 整合：将每台机器得到的最大堆合并成最终的最大堆。

@Test
public void test_topK() {
    int k = 4;
    List<Integer> array = Arrays.asList(11, 0, 9, 8, 6, 1, 4, 5, 3, 2, 7);

    PriorityQueue topKQueue = new PriorityQueue();
    for (int i = 0; i < array.size(); i++) {
        int o = array.get(i);
        if (topKQueue.size() < k) {
            //一直加到K
            topKQueue.add(o);
            System.out.println(String.format("add %s", o));
        } else {
            Object min = topKQueue.peek();
            if (o > (int) min) {
                //最小堆大小超过K且当前元素比堆顶大时，移除堆顶元素，并加入新元素
                HeapPrinter.dump(topKQueue.toArray());
                topKQueue.poll();
                topKQueue.add(o);
                System.out.println(String.format("poll %s, add %s", min, o));
                HeapPrinter.dump(topKQueue.toArray());
            } else {
                System.out.println(String.format("skip %s", o));
            }
        }
    }
}

注意：可以skip比堆顶还小的元素

求 Top k，更简单的方法可以直接用内置的TreeMap或者TreeSet，

TODO：TreeMap和TreeSet源码解析

Scanning through a large collection of statistics to report the top N items
eg.N busiest network connections, N most valuable customers, N largest disk users…

PriorityQueue在Hadoop中的应用

在 hadoop 中，排序是 MapReduce 的灵魂，MapTask 和 ReduceTask 均会对数据按 Key 排序，这个操作是 MR 框架的默认行为，不管你的业务逻辑上是否需要这一操作。

• MapReduce 框架中，用到的排序主要有两种：快速排序和基于堆实现的优先队列。
• Mapper 阶段： 从 map 输出到环形缓冲区的数据会被排序（这是 MR 框架中改良的快速排序），这个排序涉及partition和key，
  当缓冲区容量占用 80%，会spill数据到磁盘，生成IFile文件，
  Map结束后，会将IFile文件排序合并成一个大文件（基于堆实现的优先级队列），以供不同的reduce来拉取相应的数据。
• Reducer 阶段：
  从 Mapper 端取回的数据已是部分有序，Reduce Task 只需进行一次归并排序即可保证数据整体有序。
  为了提高效率，Hadoop 将sort阶段和reduce阶段并行化，
  在sort阶段，Reduce Task 为内存和磁盘中的文件建立了小顶堆，保存了指向该小顶堆根节点的迭代器，并不断的移动迭代器，
  以将 key 相同的数据顺次交给reduce()函数处理，期间移动迭代器的过程实际上就是不断调整小顶堆的过程（建堆→取堆顶元素→重新建堆→取堆顶元素…），这样，sort 和 reduce 可以并行进行。

常见问题

1. PriorityQueue的底层数组叫什么？原理是什么？如何实现排序的？
2. 如何在N（N>>10000）个数据中找到最大的K个数？要求复杂度小于O(N*N)！

参考

• jdk8.PriorityQueue
• 堆排序
• java集合之PriorityQueue源码分析
• priorityQueue元素删除问题